I promised that I would write about my solving some LeetCode problems. So here it is, my first post about LeetCode.

This was my first contest in a while. This time I decided to come back to LeetCode and contests in particular to get a Guardian badge. I don’t have one, only limited number of people have it, so why wouldn’t I try achieve this interesting goal? The conditions of getting one are quite difficult, as you need to have 1) a contest rating higher than a certain threshold 2) get into top 5% of the contest ranking. The second condition is the most difficult to get,in my opinion. I have done it only once prior to this contest, so it would be a tough one to repeat. While gaining a rating would be just a matter of a few consistent performances. With the goal of getting a badge, I have registered for the contest and here are the problems that met me:

1. 3065. Minimum Operations to Exceed Threshold Value I

This problem is probably the easiest problem I have seen at the LeetCode contest. The text of the problem is short and simple:

You are given a 0-indexed integer array nums, and an integer k. In one operation, you can remove one occurrence of the smallest element of nums. Return the minimum number of operations needed so that all elements of the array are greater than or equal to k.

Example 1:

Input: nums = [2,11,10,1,3], k = 10
Output: 3

Example 2:

Input: nums = [1,1,2,4,9], k = 1
Output: 0

To solve this problem, just iterate over a list and calculate the number of elements that don’t satisfy the condition. Simple code for the problem is below:

class Solution {
public:
    int minOperations(vector<int>& nums, int k) {
        int count = 0;
        for(auto& e : nums){
            if(e < k)
                count += 1;
        }
        return count;
    }
};

2. 3066. Minimum Operations to Exceed Threshold Value II

This problem is a slight modification of the previous problem, here is the text:

You are given a 0-indexed integer array nums, and an integer k. In one operation, you will:

• Take the two smallest integers x and y in nums.
• Remove x and y from nums.
• Add min(x, y) * 2 + max(x, y) anywhere in the array.

Note that you can only apply the described operation if nums contains at least two elements.

Return the minimum number of operations needed so that all elements of the array are greater than or equal to k.

Example 1:

Input: nums = [2,11,10,1,3], k = 10\
Output: 3

Example 2:

Input: nums = [1,1,2,4,9], k = 1\
Output: 0

Notice that operation that we are applying is predetermined by the state of array. Therefore, given an array of numbers, the only option for us is to simulate the described behavior. There is nothing that depends on us, except of efficiency and to have that, we will use priority queue. First, push all elements into priority_queue that is setup as a min-heap. Repeat operation until the condition is satisfied or there are no more elements left. My submission is below.

class Solution {
public:
    int minOperations(vector<int>& nums, int k) {
        priority_queue<unsigned int, vector<unsigned int>, greater<unsigned int>> pq;
        int count = 0;
        for(auto& e : nums)
            pq.push(e);
        while(pq.size() >= 2 && (pq.top() < k)){
            unsigned int a = pq.top();
            pq.pop();
            unsigned int b = pq.top();
            pq.pop();
            unsigned int c = min(a, b) * 2 + max(a, b);
            pq.push(c);
            count += 1;
        }
        return count;
    }
};

3. 3067. Count Pairs of Connectable Servers in a Weighted Tree Network

At first, I skipped this problem because I didn’t pay enough attention when reading the text. It seemed difficult, and having an adrenaline of keeping a good pace (done with first two problems in 0:07:45) and not willing to lose time here, I switched to problem number 4, which I loved. But let’s do this problem first.

You are given an unrooted weighted tree with n vertices representing servers numbered from 0 to n - 1, an array edges where edges[i] = [a_i, b_i, weight_i] represents a bidirectional edge between vertices a_i and b_i of weight weight_i. You are also given an integer signalSpeed.

Two servers a and b are connectable through a server c if:

• a < b, a != c and b != c.
• The distance from c to a is divisible by signalSpeed.
• The distance from c to b is divisible by signalSpeed.
• The path from c to b and the path from c to a do not share any edges.

Return an integer array count of length n where count[i] is the number of server pairs that are connectable through the server i.

Example 1:

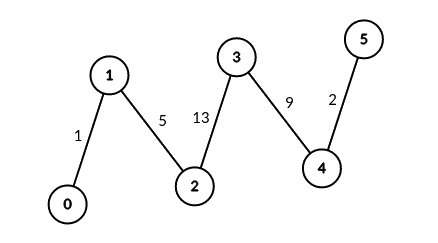
Input: edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1
Output: [0,4,6,6,4,0]

Looking back, this code can be definitely improved, but it works, so let’s try to understand it. First, construct a graph. As the requirement states, we are given a valid tree, then the only possible way for paths to share an edge, if they are in the same subtree, relatively to the current considered root. Therefore, to solve the problem we can apply the following algorithm:

1. Consider each vertices as the root.
2. Count number of vertices, that satisfy the condition of “distance from c to b is divisible by signalSpeed” in each subtree.
3. Calculate number of possible combinations, by multiplying the number of eligible vertices for each pair of the subtrees.

The code below does exactly that.

class Solution {
public:
    vector<int> countPairsOfConnectableServers(vector<vector<int>>& edges, int signalSpeed) {
        int n = edges.size() + 1;
        // Initialize the graph
        vector<vector<pair<int,int>>> g(n, vector<pair<int,int>>(0));
        vector<int> result(n, 0);
        for(auto& edge : edges){
            g[edge[0]].push_back(pair(edge[1], edge[2]));
            g[edge[1]].push_back(pair(edge[0], edge[2]));
        }
        // For each vertex, perform DFS
        for(int current = 0; current < n; current++){
            vector<vector<int>> distances(g[current].size(), vector<int>(n, -1));
            vector<int> visited(g[current].size(), 0);
            // Modified DFS, that would start from the edge, to easily check for condition 
            // of sharing any edges
            for(int start_edge_idx = 0; start_edge_idx < g[current].size(); start_edge_idx++){
                distances[start_edge_idx][current] = 0;
                distances[start_edge_idx][g[current][start_edge_idx].first] = g[current][start_edge_idx].second;
                deque<int> q_cur;
                q_cur.push_back(g[current][start_edge_idx].first);
                visited[start_edge_idx] = (g[current][start_edge_idx].second % signalSpeed == 0);
                while(!q_cur.empty()){
                    int a = q_cur.front();
                    q_cur.pop_front();
                    for(auto& edge : g[a]){
                        if(distances[start_edge_idx][edge.first] == -1){
                            q_cur.push_back(edge.first);
                            distances[start_edge_idx][edge.first] = distances[start_edge_idx][a] + edge.second;
                            if(distances[start_edge_idx][edge.first] % signalSpeed == 0)
                                visited[start_edge_idx]++;
                        }
                    }
                }
            }
            // Calculate nubmer of possible combinations
            for(int i = 0; i < g[current].size(); i++){
                for(int j = i + 1; j < g[current].size(); j++){
                    result[current] += visited[i] * visited[j];
                }
            }
        }
        return result;
    }
};

4. 3068. Find the Maximum Sum of Node Values

There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 0-indexed 2D integer array edges of length n - 1, where edges[i] = [u_i, v_i] indicates that there is an edge between nodes u_i and v_i in the tree. You are also given a positive integer k, and a 0-indexed array of non-negative integers nums of length n, where nums[i] represents the value of the node numbered i.

Alice wants the sum of values of tree nodes to be maximum, for which Alice can perform the following operation any number of times (including zero) on the tree:

• Choose any edge [u, v] connecting the nodes u and v, and update their values as follows:
  • nums[u] = nums[u] XOR k
  • nums[v] = nums[v] XOR k

Return the maximum possible sum of the values Alice can achieve by performing the operation any number of times.

I absolutely loved the problem, as it requires you to find an interesting observation about the provided operation. We can perform the given operation not only on those vertices that are connected by a direct edge, but on any pair of two vertices that have a path in between. The given structure of edges is a valid tree according to the requirements, therefore this operation can be applied on any pair of vertices. Let’s figure out why this works.

First of all, XOR has a property we are interested in which is a XOR b XOR b = a, as b XOR b = 0. If there is a path between a and b of form

a -- c_1 -- c_2 -- ... c_n -- b

we can apply n + 1 operations for each pair of neighbor and get values of

a XOR k -- c_1 -- c_2 -- ... c_n -- b XOR k

as a and b are going to be teh only vertices to which operation will be applied once.

Having improved our understanding of this operation, let’s try maximize value sum with the new knowledge. After applying operations, each vertex can have only 1 one of the 2 value – nums[i] or nums[i] XOR k. Let’s sum the maximum of the two for each of the vertices. This would result in the correct answer, if the number of cases where nums[i] < nums[i] XOR k is even. In the it is odd, we need to either get rid of the entry with maximum nums[i] - nums[i] XOR k by replacing its nums[i] XOR k with nums[i] or get rid of the entry with minimum nums[i] XOR k - nums[i] by replacing its nums[i] with nums[i] XOR k. In this way, we would minimize the loss in the sum in order to satisfy the conditions, which is equivalent to maximizing the sum.

The code below implements the presented algorithm.

class Solution {
public:
    long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {
        long long total_sum = 0;
        int such_that = 0;
        int minimum_gain = 1e9;
        int minimum_loss = 1e9;
        for(int i = 0; i < nums.size(); i++){
            if((nums[i] ^ k) > nums[i]){
                such_that++;
                total_sum += nums[i] ^ k;
                minimum_gain = min((nums[i] ^ k) - nums[i], minimum_gain);
            } else{
                minimum_loss = min(nums[i] - (nums[i] ^ k), minimum_loss);
                total_sum += nums[i];
            } 
        }
        if(such_that % 2 == 0)
            return total_sum;
        return total_sum - min(minimum_gain, minimum_loss);
    }
};

What’s funny about it, is that we even haven’t used edges in any way, as we found the invariant of the operation.

Retrospective

Looking back, this was a good way to get back into LeetCode contests, as I solved all of the problems. Being excited after the contest, I also decided to stay up until 5AM to also participate in the Weekly Contest which is in the US timezone, where I also solved all of the problems. In order to improve my ranking in the contests, I need to have less bad submission, as I get at least a couple in each contest. I need to be more attentive and spend a bit more time debugging the solution, rather than submit the solution straight away.

As the result fo 2 contests, I improved my rating by +45 as the result of the Biweelky contest and +12 as the result of the Weekly contest, adding up to a total +57 in a single weekend. Stay tuned for the next parts, as I am on the way to achieve the Guardian badge.

I will also spend more time on my personal projects and articles about them are coming as soon as I polish them enough. You don’t want to see ugly code and design choices, right? :)